Monthly Archives: March 2017

YouTube Yikes!

Posted on March 18, 2017 by Anshul Kogar | Leave a comment

A couple days ago, Lawrence Livermore National Laboratory released a number of videos of nuclear test explosions. It is worth watching some of these to understand the magnitude of destruction that these can cause. Here is a link to the Lawrence Livermore playlist on YouTube, and below is a video explaining a bit of the background concerning the release of these videos:

Below is a helpful MinutePhysics video that talks about the actual dangers concerning nuclear weapons:

On a somewhat unrelated note, while at the APS March Meeting this past week, Peter Abbamonte mentioned this video to me, which I also found pretty startling:

Lastly, here is a tragicomedy that takes place in the wild — it seems like this orca was never told by its mother not to play with its food:

https://twitter.com/NatureisScary/status/805247043350433792

Zener’s Electrical Breakdown Model

Posted on March 12, 2017 by Anshul Kogar | Leave a comment

In my previous post about electric field induced metal-insulator transitions, I mentioned the notion of Zener breakdown. Since the idea is not likely to be familiar to everyone, I thought I’d use this post to explain the concept a little further.

Simply stated, Zener breakdown occurs when a DC electric field applied to an insulator is large enough such that the insulator becomes conducting due to interband tunneling. Usually, when we imagine electrical conduction in a solid, we think of the mobile electrons moving only within one or more partially filled bands. Modelling electrical transport within a single band can already get quite complicated, so it was a major accomplishment that C. Zener was able to come up with a relatively simple and solvable model for interband tunneling.

To make the problem tractable, Zener came up with a hybrid real-space / reciprocal-space model where he could use the formalism of a 1D quantum mechanical barrier:

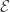In Zener’s model, the barrier height is set by the band gap energy, $E_{g}$ , between the valence and conduction bands in the insulator, while the barrier width is set by the length scale relevant to the problem. In this case, we can say that the particle can gain enough kinetic energy to surpass the barrier if $e\mathcal{E}d = E_{g}$ , in which case our barrier width would be:

$d = E_{g} / e\mathcal{E}$ ,

where $\mathcal{E}$ is the applied electric field and $e$ is the electron charge.

Now, how do we solve this tunneling problem? If we were to use the WKB formalism, like Zener, we get that the transmission probability is:

$P_T = e^{-2\gamma}$ where $\gamma = \int_0^d{k(x) dx}$ .

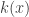Here, $k(x)$ is the wavenumber. So, really, all that needs to be done is to obtain the correct funtional form for the wavenumber and (hopefully) solve the integral. This turns out not to be too difficult — we just have to make sure that we include both bands in the calculation. This can be done in similar way to the nearly free electron problem.

Quickly, the nearly-free electron problem considers the following $E-k$ relations in the extended zone scheme:

E-kRelation

Near the zone boundary, one needs to apply degenerate perturbation theory due to Bragg diffraction of the electrons (or degeneracy of the bands from the next zone, or however you want to think about it). So if one now zooms into the hatched area in the figure above, one gets that a gap opens up by solving the following determinant and obtaining $\epsilon(k)$ :

$\left( \begin{array}{cc} \lambda_k - \epsilon & E_g/2 \\ E_g/2 & \lambda_{k-G} - \epsilon \end{array} \right)$ ,

where $\lambda_k$ is $\hbar^2k^2/2m$ in this problem, and the hatched area becomes gapped like so:

ZoneBoundaryGap

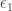In the Zener model problem, we take a similar approach. Instead of solving for $\epsilon(k)$ , we solve for $k(\epsilon)$ . To focus on the zone boundary, we first let $k \rightarrow k_0 + \kappa$ and $\epsilon \rightarrow \epsilon_0 + \epsilon_1$ , where $k_0 = \pi/a$ (the zone boundary) and $\epsilon_0 = \hbar^2k_0^2/2m$ , under the assumption that $\kappa$ and $\epsilon_1$ are small. All this does is shift our reference point to the hatched region in previous figure above.

The trick now is to solve for $k(\epsilon)$ to see if imaginary solutions are possible. Indeed, they are! I get that:

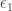$\kappa^2 = \frac{2m}{\hbar^2} (\frac{\epsilon_1^2 - E_g^2/4}{4\epsilon_0})$ ,

so as long as $\epsilon_1^2 - E_g^2/4 < 0$ , we get imaginary solutions for $\kappa$ .

Although we have a function $\kappa(\epsilon_1)$ , we still need to do a little work to obtain $\kappa(x)$ , which is required for the WKB exponent. Here, Zener just assumed the simplest thing that he could, that $\epsilon_1$ is related to the tunneling distance, $x$ , linearly. The image I’ve drawn above (that shows the potential profile) and the fact that work done by the electric field is $e\mathcal{E}x$ demonstrates that this assumption is very reasonable.

Plugging all the numbers in and doing the integral, one gets that:

$P_T = \exp-\left(\pi^2 E_g^2/(4 \epsilon_0 e \mathcal{E} a)\right)$ .

If you’re like me in any way, you’ll find the final answer to the problem pretty intuitive, but Zener’s methodology towards obtaining it pretty strange. To me, the solution is quite bizarre in how it moves between momentum space and real space, and I don’t have a good physical picture of how this happens in the problem. In particular, there is seemingly a contradiction between the assumption of the lattice periodicity and the application of the electric field, which tilts the lattice, that pervades the problem. I am apparently not the only one that is uncomfortable with this solution, seeing that it was controversial for a long time.

Nonetheless, it is a great achievement that with a couple simple physical pictures (albeit that, taken at face value, seem inconsistent), Zener was able to qualitatively explain one mechanism of electrical breakdown in insulators (there are a few others such as avalanche breakdown, etc.).

Mott Switches and Resistive RAMs

Posted on March 4, 2017 by Anshul Kogar | 1 comment

Over the past few years, there have been some interesting developments concerning narrow gap correlated insulators. In particular, it has been found that it is particularly easy to induce an insulator to metal transition (in the very least, one can say that the resistivity changes by a few orders of magnitude!) in materials such as VO₂, GaTa₄Se₈ and NiS_2-xS_x with an electric field. There appears to be a threshold electric field above which the material turns into a metal. Here is a plot demonstrating this rather interesting phenomenon in Ca₂RuO₄, taken from this paper:

It can be seen that the transition is hysteretic, thereby indicating that the insulator-metal transition as a function of field is first-order. It turns out that in most of the materials in which this kind of behavior is observed, there usually exists an insulator-metal transition as a function of temperature and pressure as well. Therefore, in cases such as in (V_1-xCr_x)₂O₃, it is likely that the electric field induced insulator-metal transition is caused by Joule heating. However, there are several other cases where it seems like Joule heating is likely not the culprit causing the transition.

While Zener breakdown has been put forth as a possible mechanism causing this transition when Joule heating has been ruled out, back-of-the-envelope calculations suggest that the electric field required to cause a Zener-type breakdown would be several orders of magnitude larger than that observed in these correlated insulators.

On the experimental side, things get even more interesting when applying pulsed electric fields. While the insulator-metal transition observed is usually hysteretic, as shown in the plot above, in some of these correlated insulators, electrical pulses can maintain the metallic state. What I mean is that when certain pulse profiles are applied to the material, it gets stuck in a metastable metallic state. This means that even when the applied voltage is turned off, the material remains a metal! This is shown here for instance for a 30 microsecond / 120V 7-pulse train with each pulse applied every 200 microseconds to GaV₄S₈ (taken from this paper):

Electric field pulses applied to GaV₄S₈. A single pulse induces a insulator-metal transition, but reverts back to the insulating state after the pulse disappears. A pulse train induces a transition to a metastable metallic state.

Now, if your thought process is similar to mine, you would be wondering if applying another voltage pulse would switch the material back to an insulator. The answer is that with a specific pulse profile this is possible. In the same paper as the one above, the authors apply a series of 500 microsecond pulses (up to 20V) to the same sample, and they don’t see any change. However, the application of a 12V/2ms pulse does indeed reset the sample back to (almost) its original state. In the paper, the authors attribute the need for a longer pulse to Joule heating, enabling the sample to revert back to the insulating state. Here is the image showing the data for the metastable-metal/insulator transition (taken from the same paper):

gava4s8_reset

So, at the moment, it seems like the mechanism causing this transition is not very well understood (at least I don’t understand it very well!). It is thought that there are filamentary channels between the contacts causing the insulator-metal transition. However, STM has revealed the existence of granular metallic islands in GaTa₄S₈. The STM results, of course, should be taken with a grain of salt since STM is surface sensitive and something different might be happening in the bulk. Anyway, some hypotheses have been put forth to figure out what is going on microscopically in these materials. Here is a recent theoretical paper putting forth a plausible explanation for some of the observed phenomena.

Before concluding, I would just like to point out that the relatively recent (and remarkable) results on the hidden metallic state in TaS₂ (see here as well), which again is a Mott-like insulator in the low temperature state, is likely related to the phenomena in the other materials. The relationship between the “hidden state” in TaS₂ and the switching in the other insulators discussed here seems to not have been recognized in the literature.

Anyway, I heartily recommend reading this review article to gain more insight into these topics for those who are interested.

1 Comment

Posted in Mott Insulators, Research, Review

Tagged Experiment, Mott Insulators, Research, Review